Atmospheric Scattering

This article is reproduced for posterity from codeflow.org, which is now no longer online. It explains how to render a realistic sky in GLSL by ray‐marching through a simplified spherical atmosphere.

Live Demo Link

Contents

Repository

https://github.com/binaryfoundry/atmospheric-scattering

Demo

Live Demo Link

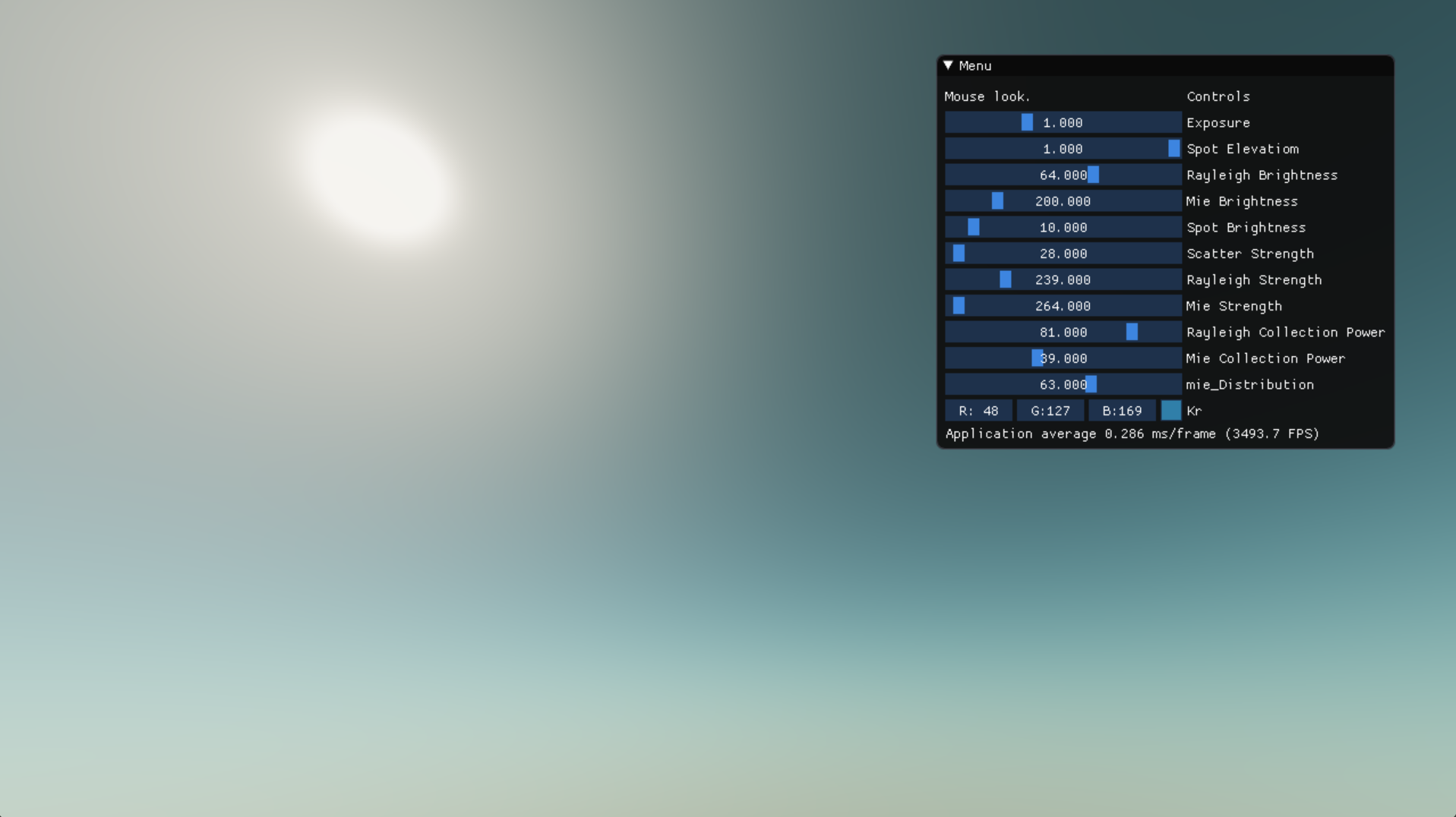
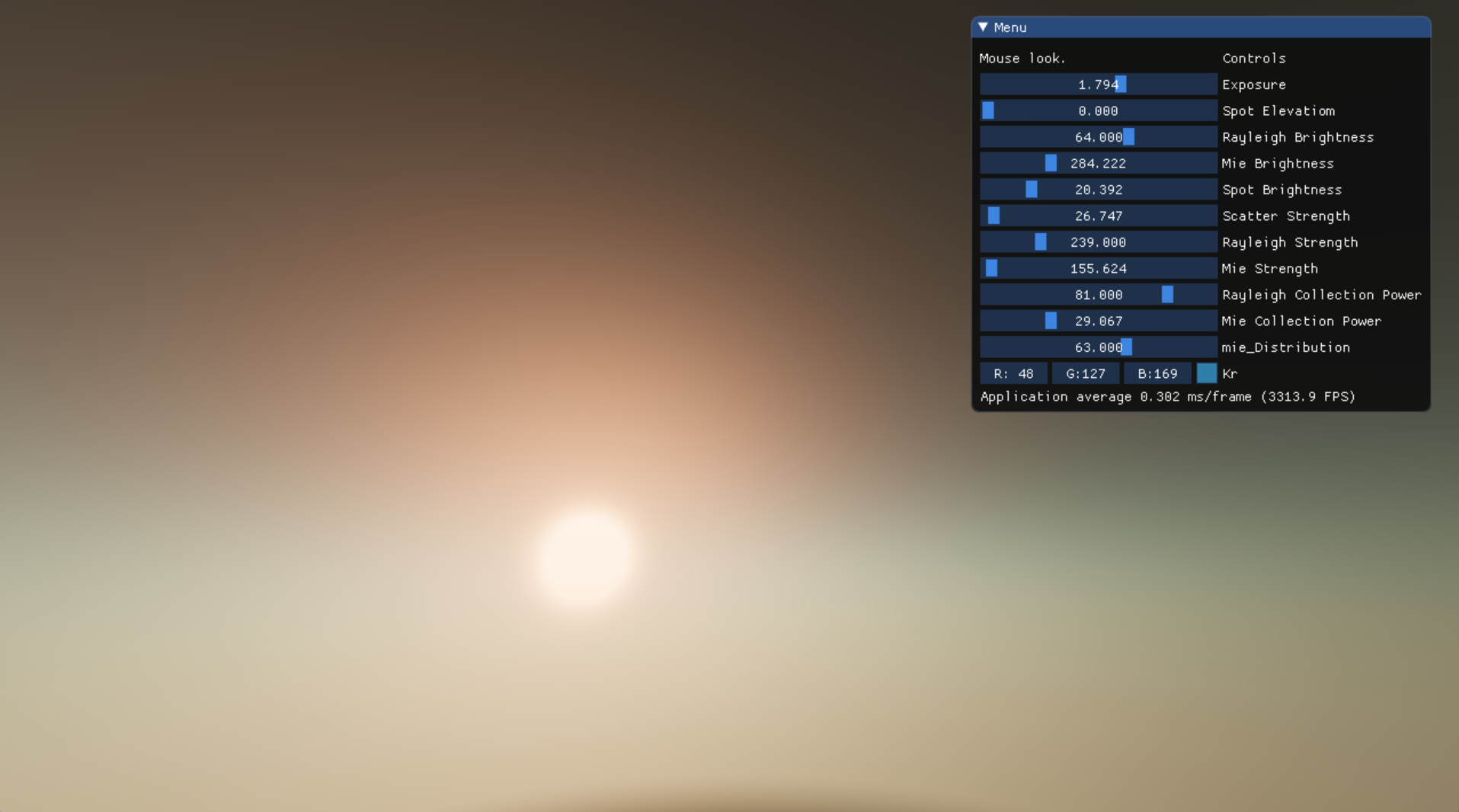
Screenshots

Overview

The idea is to trace a ray for each pixel from the observer position. Along a fixed number of sampling points along that ray, rays are shot towards the sun. The depth of atmosphere traversed is measured. So the collected light at each sample point is known, and hence the reflected light (towards the observer) can be calculated.

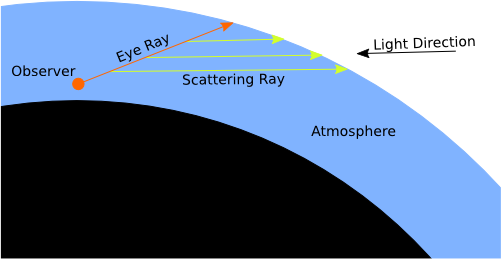
This GPU Gem gives a much better description of the algorithm than I could give.

Setup

I am rendering the atmospheric scattering into a FBO by drawing two screen‐filling triangles. This is a common technique for other effects and post processing, and it avoids me having to draw a planet‐sized sphere for the atmosphere.

The target I use for the FBO is a cubemap. This helps me avoid having to render the sky every frame. I can just refresh the sky when it changes.

The atmosphere is assumed to be of constant density. This is certainly wrong, but taking atmospheric density into account makes it much more difficult to compute the effect.

Eye Ray

In order to determine the eye ray (in world coordinates) you will need the viewport dimensions, the inverse projection matrix, and the inverse view rotation matrix. I pass these variables in as uniforms to the shader. Given this information, the following function derives the eye ray from the gl_FragCoord.

vec3 get_world_normal() {
    vec2 frag_coord = gl_FragCoord.xy / viewport;
    frag_coord = (frag_coord - 0.5) * 2.0;
    vec4 device_normal = vec4(frag_coord, 0.0, 1.0);
    vec3 eye_normal = normalize((inv_proj * device_normal).xyz);
    vec3 world_normal = normalize(inv_view_rot * eye_normal);
    return world_normal;
}

Reflection

Due to the nature of molecular reflection, light does not bounce off small particles and molecules the way it bounces off solid surfaces. For Nitrogen it bounces least if you are perpendicular to the incoming light direction. And for aerosols (dust/water) it bounces strongest the smaller the angle between the light and viewing direction.

First you need to figure out the angle between the viewing direction and the light:

vec3 eyedir = get_world_normal();
float alpha = dot(eyedir, lightdir);

Then you need a phase function to calculate different kinds of reflections. This is taken straight from this cool GPU Gem:

float phase(float alpha, float g) {
    float a = 3.0 * (1.0 - g * g);
    float b = 2.0 * (2.0 + g * g);
    float c = 1.0 + alpha * alpha;
    float d = pow(1.0 + g * g - 2.0 * g * alpha, 1.5);
    return (a / b) * (c / d);
}

Now I can compute different factors. For lack of better naming, I call the Nitrogen profile “rayleigh,” and the aerosol profile “mie.” I also added one with which I can control a kind of sun‐spotlight.

float rayleigh_factor = phase(alpha, -0.01) * rayleigh_brightness;
float mie_factor       = phase(alpha, mie_distribution) * mie_brightness;
float spot             = smoothstep(0.0, 15.0, phase(alpha, 0.9995)) * spot_brightness;

Atmospheric Depth

I need to figure out the depth a ray traverses from a given point in a given direction inside a sphere. For simplicity’s sake the sphere is assumed to always be of radius 1.

If you substitute the formula of the vector into the formula of the sphere, you can arrive at the solution—nicely described by this article.

float atmospheric_depth(vec3 position, vec3 dir) {
    float a = dot(dir, dir);
    float b = 2.0 * dot(dir, position);
    float c = dot(position, position) - 1.0;
    float det = b * b - 4.0 * a * c;
    float detSqrt = sqrt(det);
    float q = (-b - detSqrt) / 2.0;
    float t1 = c / q;
    return t1;
}

Note that I’m assuming we are inside the sphere, so I know that the determinant is always greater than 0. And since I’m interested in the first intersection along the ray, I can forget about the rest of the quadratic formula.

Using this formula I can now calculate the depth of the eye ray and how long each sample step is going to be:

vec3 eye_position = vec3(0.0, surface_height, 0.0);
float eye_depth    = atmospheric_depth(eye_position, eyedir);
float step_length  = eye_depth / float(step_count);

Horizon Extinction

Due to the fact that solid bodies block light, I should really have some function that can tell me how much a ray is occluded as well. After some experimentation I settled on projecting the ray direction onto the negative position. If u (the factor by which to multiply position) is greater than 0, the ray points above the horizon. If it’s smaller than some given radius, then it’s assumed to be completely occluded. In between, some crude approximation to angular extinction is used that I arrived at after more experimenting. I’m pretty sure there are better ways to solve the problem, but this one was easy to implement.

float horizon_extinction(vec3 position, vec3 dir, float radius) {
    float u = dot(dir, -position);
    if (u < 0.0) {
        return 1.0;
    }
    vec3 near = position + u * dir;
    if (length(near) < radius) {
        return 0.0;
    } else {
        vec3 v2   = normalize(near) * radius - position;
        float diff = acos(dot(normalize(v2), dir));
        return smoothstep(0.0, 1.0, pow(diff * 2.0, 3.0));
    }
}

I can use this function to compute a factor for how much the eye ray is occluded:

float eye_extinction = horizon_extinction(
    eye_position,
    eyedir,
    surface_height - 0.15
);

I choose a small radius (0.15) smaller than the surface height, which makes it smooth and extends a bit beyond the horizon (this is very practical for games).

The color of air

You can look up the factors of absorption for different gases. I used the absorption profile for Nitrogen which looks like this:

vec3 Kr = vec3(
    0.18867780436772762,
    0.4978442963618773,
    0.6616065586417131
);

As you can see, it absorbs a lot of blue light, which means that if something travels a lot through the atmosphere it gets redder. This is also the same profile you use to reflect, and hence the sky appears blue.

Collecting the Light

I need some variables to hold the collected light. Since Nitrogen and aerosols reflect differently, I need two of them:

vec3 rayleigh_collected = vec3(0.0, 0.0, 0.0);
vec3 mie_collected      = vec3(0.0, 0.0, 0.0);

Then I run a loop for a given number of steps which runs along the eye ray in the previously calculated step length:

for (int i = 0; i < step_count; i++) {
    float sample_distance = step_length * float(i);
    vec3 position         = eye_position + eyedir * sample_distance;
    float extinction      = horizon_extinction(
        position,
        lightdir,
        surface_height - 0.35
    );
    float sample_depth = atmospheric_depth(position, lightdir);
}
  • sample_distance is the distance from the observer to the sample.
  • position is the sample’s position inside the sphere.
  • extinction is how much that sample is occluded toward the light.
  • sample_depth is the distance from the sample point to the border of the atmosphere.

Light Absorption

I modeled the light absorption inside the atmosphere as an exponential function of the inverse depth. It’s exponential because if light traverses a certain distance and 50% gets absorbed, then traverses the same distance again, another 50% of the remainder gets absorbed:

vec3 absorb(float dist, vec3 color, float factor) {
    return color - color * pow(Kr, vec3(factor / dist));
}

The idea is: given a color, a certain amount of that color is absorbed. The smaller the distance, the less is absorbed. The power is taken to the base Kr, which is the color distribution of air (absorbs slightly reddish).

In the loop I first absorb light for the sample ray from the sun to the sample position (I call this influx):

vec3 influx = absorb(sample_depth, vec3(intensity), scatter_strength) * extinction;

Then I multiply that influx with Kr for the Nitrogen reflection and leave it as-is for the Mie (aerosol) collection. This gets absorbed again by the distance of the sample to the observer:

rayleigh_collected += absorb(
    sample_distance,
    Kr * influx,
    rayleigh_strength
);
mie_collected += absorb(
    sample_distance,
    influx,
    mie_strength
);

Finishing Up

Each collected result needs to be multiplied by the eye extinction. It is also divided by step_count to normalize the value. Multiplication by eye_depth simulates that the longer a ray travels in the atmosphere, the more light it can return (because more particles between it and the observer reflected some light). Raising to a power is used for fine-tuning:

rayleigh_collected = (
    rayleigh_collected *
    eye_extinction *
    pow(eye_depth, rayleigh_collection_power)
) / float(step_count);

mie_collected = (
    mie_collected *
    eye_extinction *
    pow(eye_depth, mie_collection_power)
) / float(step_count);

Finally, the color is the summation of the collected light with the reflection distribution factors:

vec3 color = vec3(
    spot * mie_collected +
    mie_factor * mie_collected +
    rayleigh_factor * rayleigh_collected
);

Fine Tuning

You might have noticed that at various parts I use passed-in uniforms. The purpose of this is artistic fine-tuning of the result. A more accurate simulation could reduce some of these tuning parameters.

Written on June 2, 2025