In the future coding job interviews might not only ask questions about basic time-complexity such as Big O, but involve intractable problems and how to approximate solutions in realistic time-frames. Or to put it a little more bluntly, employers will want to know if you have some machine learning knowledge.

This post is about a very simple learning algorithm called Q-Learning, although simple it can be used to effectively tackle problems such as elevator scheduling, and is the underlying idea behind Alpha Go, DeepMind’s Go playing AI. The Tic Tac Toe game below has an opponent trained using Q-Learning, the algorithm should find a good strategy, try it out!

Despite its simplicity, compiling information on Q-Learning did take some time, sources are listed in references at the end of this post ¹². Many explanations get distracted talking about agents, environments, policies, game theory and other topics which are tangentially related. This post will instead focus on the Bellman Function which is what makes Q-Learning tick.

Terms

The initial “state” in our given case is an empty Tic Tac Toe board, each player takes a turn or “action” to put the board in to a new “state.”

Q-Learning can be used learn how to best take an action to move from one state to another when:

• Only the current state, not previous states matter. There is no dependency on things which have already happened.
• Rules do not change. For example in the Tic Tac Toe game, the winner always has to make a line of 3, this never changes.

When a process satisfies these two conditions it has The Markov Property. Q-Learning will discover the best action policy in a Markov Decision Process, which for us is a Tic Tac Toe playing AI.

The Bellman Equation

From each position on the maze below, a choice of four actions can be made, to move up, down, left or right. If we want to move from the top left corner to the bottom right, we initially don’t know if a choice of any of these actions can ultimately move us closer to our goal. So we choose an action randomly until the goal is reached.

The goal has a reward value, let’s say 100. Once the goal is discovered we take the reward value, reduce it by a percentage, and pass it back to the previous state. Eventually the reward will propagate through back to the starting state at a much reduced value. Now if the reward was cheese a mouse could find it’s way optimially through the maze by following the smell of cheese at it gets stronger, the strength of the smell is the “Q” value.

More accurately, for a state The Bellman Equation is:

Q = StateReward + LearningRate * MaximumQFromStatesAvailableActions

This HTML5 demo shows the “Q” value propagating through a maze using The Bellman Function. An addition action decision has been added to make the mouse agent perfer to explore new areas than re-tread old ground.

Tic Tac Toe

Training the AI for Tic Tac Toe works in exactly the same way, turns are made randomly until a goal win state is found. The reward propagates back to the initial state so the AI knows the best actions to take. Here is a visualization of the training process.

Strategy

As it stands the current training process is close to brute force, with probably all combinations being explored. It is easy to just check every possible state in Tic Tac Toe, so discovering the best policy by training is really just proof by exhaustion.

Therefore it’s easy to know two expert players can always block each-other from winning, so instead of acting of the best policy that results in a win, the best action to stop the other player from winning is chosen. This results in a much better overall strategy.

Also the Q value for two actions ahead is factored in, since players take turns.

Attacking Training Complexity

But what if there are too many combinations to check? A best guess will have to suffice. Instead of just randomly moving, over time the agent could begin to prefer exploring actions with higher Q values, cooling off the randomness until training completes.

This concept is similar to Simulated Annealing ³. In a heated metal, excited energy will jump around with a high degree of randomness, as the metal cools and energy jumps less excitedly, it will pool in denser areas of the metal.

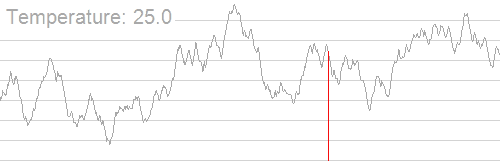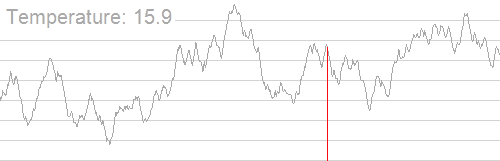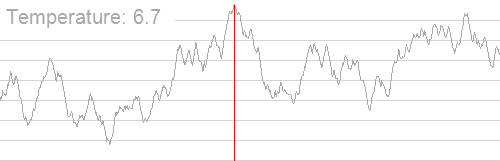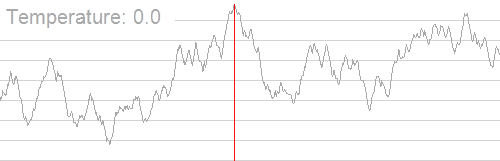
• “Simulated annealing searching for a maximum. The objective here is to get to the highest point; however, it is not enough to use a simple hill climb algorithm, as there are many local maxima. By cooling the temperature slowly the global maximum is found.” ⁴

Conclusion

Q-Learning can be used to make effective AIs in a very simple way. Simple enough to provide satisfactory approximate solutions to difficult problems that could be found in job interviews.

References